How To Split Rent With Your Flatmate

Hyderabad, June 24

My Analysis professor liked to say, “Elementary does not mean easy!”.

I have spent roughly 2 years (intermittently) pondering this problem. It is time to write about it, so I can, at least for a short while, be free of it. This is a problem a lot of us encounter in daily life, but I have yet to see an elegant solution. Maybe mechanism design can help us.

Mechanism design is frequently called the inverse of game theory. The description often used is as follows: “In game theory, you start with a game (an interaction between participants), play out the actions taken by the participants to maximize their own benefit and calculate the outcome. Mechanism design involves starting with a desired outcome and designing a game such that, when people play the game to the best of their ability, you achieve the desired outcome.” While broadly true, this is slightly misleading, as most of mechanism design is several and repeated applications of what we normally understand as game theory. Yet, I use that phrasing myself as it makes for good conversation and is much more accessible than the nuances outlined here. You may also do the same, and hope no one calls you out for propagating imprecise memes.

Mechanism design is also one-half of what makes a blockchain (like Bitcoin) work.

The Problem

Anyway, let’s get straight to the problem. It is motivated by my own situation when I first moved to Bangalore a few years ago. I was sharing an apartment that had 2 rooms. We had a smaller room with an attached bathroom, and a slightly larger room with an external bathroom.

My flat in Bangalore

The two rooms were different, but neither was necessarily objectively better than the other. This is crucial and expected, because you can never have two rooms that are exactly the same — they would simply collide in spacetime. There is another way in which the rooms are different, from the perspective of mine and my roommate’s intrinsic valuation for the rooms. More on this later. For now, I will invoke the mechanism designer’s license to note that the apartment was (surprisingly conveniently for our purposes) available for exactly $1,000/mo.

Now at this point it may be reasonable to wonder what the fuss is about. Why don’t we just toss a coin and split the rent, since the rooms were mostly similar? If that is your thought also, I congratulate you on your socially well-adjusted life. You may safely stop reading now and go play Padel with your many friends.

For the rest of us, I will set up a little bit of a framework. What I mean by different and why I say it is crucial, is that the rooms are such that both people may value each in private differently. The two people in our story are A (me) and B (my flatmate). A privately values room 1 at a certain rate, room 2 at a certain rate and so does B. We represent this in a 2x2 grid, with example valuations:

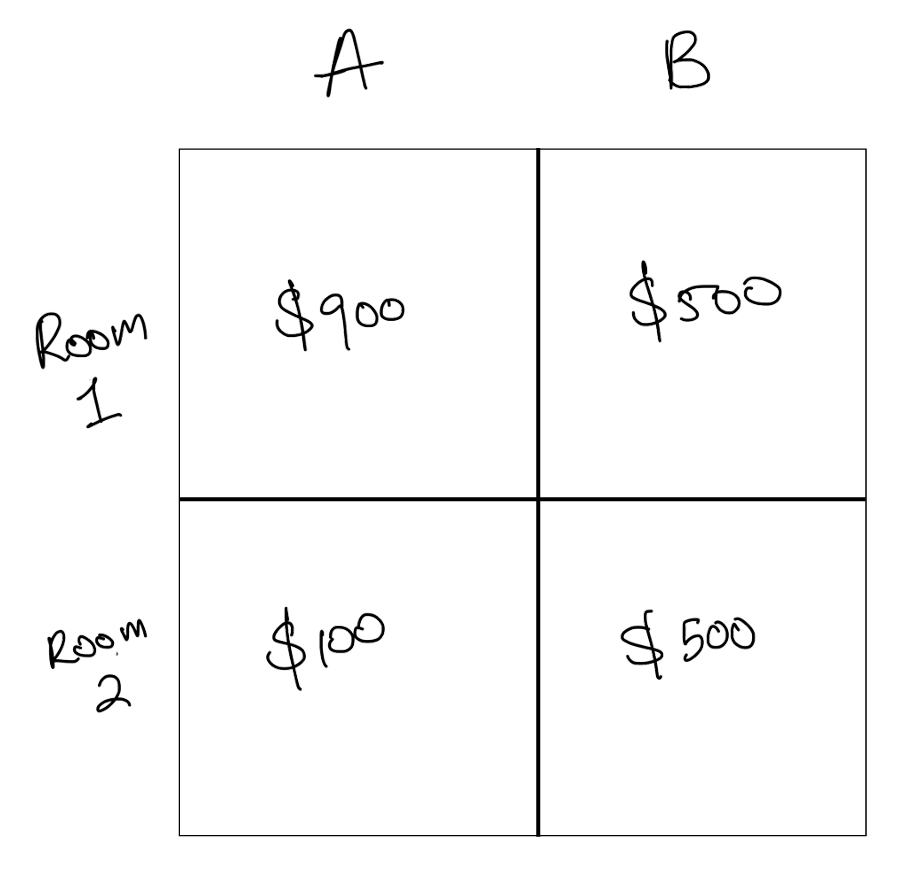
Figure 1: A really likes Room 1, while B is exactly indifferent between the two rooms

The problem is actually composed of two subproblems:

• Who gets which room (the allocation problem)
• How much does each pay for the room they are allocated (the payments problem)

Well, it's not immediately clear that there is a problem here. Indeed, the problem only arises when we put some constraints on the outcomes of the allocation: what outcome do we want, and how do we design a "game" so that we can achieve the desired outcome? To explore desired outcomes, we will begin by running through a few mechanisms and evaluating the quality of outcomes to develop some taste for what looks like a good outcome.

It is exciting because I have cycled through a few mechanisms and have realized they don't work as you would want them to. But towards the end, I will be with you, because I haven't resolved it yet. It is my fervent hope that writing this out will discover it for me.

Mechanism 1: 50-50 split

We first consider the simple obvious solution I disregarded above. Say we toss the coin and split the rent 50-50. Say the valuations are as in Figure 1 above. Basically, A really wants room 1, while B is indifferent. Two scenarios can occur. In both cases, the rent paid by each party is the same.

• A Gets Room 1: A pays $500 and receives a room that he values at $900. B pays $500 and receives a room worth $500. There is a total surplus of +$400, and A gets all of it.
• A Gets Room 2: A pays $500 for a room they only value at $100, while B pays $500 for a room worth $500. There is a total negative of -$400, and A bears all of it.

There are 2 problems with the game above — first, the outcome is highly dependent on the result of the coin toss. Second, the cumulative benefit (or loss) in each case is borne by just 1 person. Surely, we can do better.

Mechanism 2: Split the Pie

Say we have a mechanism where A decides the rents for each room, and later B chooses which room + rent they want to pay. This mechanism is an analog of the classic Pie split mechanism called Divide and Choose. Assuming A is completely rational, and does not know anything about B’s preferences — let’s explore the best game A can design. Unfortunately, this is not easy — since profitability for A depends significantly on B’s value function. Without getting into probabilities and expectations, we can show that the “safest” game that A can design is actually their own valuation. In Figure 1’s example, A gives B the option to pay $900 for Room 1 and $100 for Room 2. Clearly B has a massive advantage, and proceeds to pocket the $400 surplus by paying $100 for Room 2.

This appears to be a terrible disadvantage of this mechanism. It is also interesting that the pie splitting mechanism more generally suffers from this inadequacy — the player that chooses (goes second) always pockets any available surplus arising from differing private valuations — and is not as fair as I had initially thought.

Mechanism 3: Auctions

Now, sufficiently motivated by the failure of previous mechanisms, we turn to open the mechanism designer’s can of worms. Auctions come in many different forms. If you’re a fellow cryptography brother who’s been screaming “auction” since the beginning, I will show you it is not trivial.

We will not be discussing the regular first-price auction (what most of us think of as an auction) here since it has shown to be sub-optimal in its properties, but let’s consider a simple Vickrey (second-price) auction.

3.1 Vickrey Auction

In our classic scenario, say we auction room 1. The second-price auction says that the person with the highest bid wins the room, and the amount they pay is equal to the second-highest bid. Take this to the case of auctioning room 1, without proving why this is safest, let’s assume that both parties bid their “true valuations”. A bids $900 and B bids $500. A wins, and has to pay $500 — pocketing the difference as in Mechanism 1. On the other hand, if we had auctioned room 2, B would be the winner and would have pocketed the $400, as in Mechanism 2.

I don’t believe all hope is lost yet, though. Perhaps the Vickrey auction just requires a modification. I have a feeling this mechanism is approaching a desirable solution, and we just need to adjust the “payments”. It is also intuitively obvious that the payment function should depend on the total rent ($1,000) of the apartment.

3.2 “Mean price” auction

Let’s explore if there is a way we can design the auction such that we can split the surplus. A simple way to do this would be exactly this — the highest bidder is allocated the room, and the price paid is the average of the first two bids. In our case, if we auction room 1 (and assuming both parties “bid truthfully”), A gets room 1 for $700, and B gets room 2 for the remaining $300. Further, if we auction room 2, we get the exact same outcome — B wins the bid at $500 for room 2, and has to pay $300. I have to pay the remaining $700. This is better. The surplus is split evenly between the two parties. There is a neat symmetricity of outcome independent of the choice of room selected for auctioning. We’ve made progress!

Are we done? Unfortunately not (we’re far from it), there is one class of edge-cases we must handle. If you look carefully at the valuation function for A and B, something weird stands out. The valuations for A sum exactly to $1000 and so also for B. This is an unreasonable assumption: there is no reason the sum of my intrinsic valuations for the two rooms should exactly equal the rent of the flat. In fact, it is highly unlikely.

Let’s consider this edge case and see if we can modify our auction to account for this. Say instead of $900 and $100, my private valuations were $900 and $300. What happens in the mean price auction if I use the same bidding strategy as above? If we auction room 1, we have the same outcome as before, A gets room 1 for $700 and B gets room 2 for the remaining $300. If we auction room 2, B gets room 2 for $400 and A gets room 1 for the remaining $600. In a phrase that could easily be attributed to our glorious world leader: WEIRD!

We just lost beautiful symmetricity — we have different outcomes depending on which room is auctioned. All hope appears lost and despair rears its ugly head. Wait. Can I modify my bidding strategy to get a more equitable outcome? Let’s say I bid $800 for room 1 and $200 for room 2. What happens now? If the auction is for Room 1, I pay $650 for room 1, with a $250 surplus. If the auction is for room 2, I pay $650 for room 1 again! I have effectively hedged my inherent surplus. It is also trivial to show that this bidding strategy works just as well if applied to Mechanism 2 above.

Okay, What Does This Really Mean?

Where does this actually work, and what is the takeaway? Simply, it is this. When you show up to college, and you have to split rent with your roommate, follow this process:

1. Do not befriend them before deciding on rooms! This is crucial.
2. Write out (in private) what you each individually think the rooms are worth. For example, you may write your valuation as $600 and $300 for each room, while the total rent is $800. Your flatmate might write $500 and $500.
3. “Normalize” each person’s bids so that they each sum to $800. Effectively, consider the inherent surplus ($600 + $300 - $800 = $100 for you, and $1000-$800=$200 for your flatmate) and subtract half of this value from both bids. You now end up with $550, $250 (you) and $400/$400 (your flatmate).
4. Now you randomly select a room and apply the mean-price auction. Say we auction room 1, we end up with you winning the bid and paying $475. Your surplus here is $125. Your flatmate pays $325 for room 2. They have a surplus of $175. In the opposite case, if room 2 is selected — your flatmate wins, and pays $325. You pay $475 for room 1. Again the surpluses are the same!

Is it unfortunate or a failure of this mechanism that your flatmate has a higher surplus? No, turns out they're just a happier person (as evidenced by their higher intrinsic valuations). 🙂 You should probably take up meditation or something.

It is (to me) remarkable that this mechanism has emerged. It is genuinely in the process of writing this out that the fog has cleared. It has made my day.

Caveats

The biggest complaint I have with economic models is that they usually have nothing to do with reality, because the assumptions required to make a simple model work are so numerous that we often end up with a beautiful result in an impractical, toy scenario. Have we also suffered this terrible fate today? Hopefully not. Let’s list our assumptions here:

1. A and B do not know anything about each other’s valuation functions. This is a very important one. I am extremely interested in exploring how you design a game where you actually do know the other person’s valuation function pretty well, and the mechanics of designing games in that situation. Sharing a room with your brother, or a long-time girlfriend or partner, for example. But this is not what we are dealing with today.
2. Given 1, A and B both want to minimize their loss as opposed to swinging for potential gain. Imagine if we apply 3.2 to auction room 1 again, but that B lies about their valuation. Say that the bid is higher ($600 for example). The only cases where this changes the allocation outcome as opposed to truthful bidding is when A’s valuation is between $500-$599. If it is indeed something like $520, then B gets the room but pays $560, with a loss of -$60. Conversely if B bids lower than $500, say $400, he allows A to pay $50 less for Room 1. This is simple, if you know you’re going to win the bid, bid lower. If you know you’re going to lose the bid, bid higher than is truthful. The difference between this and a typical auction is that here, we have 2 simultaneous auctions being conducted at the same time — one for Room 1 and one for Room 2, even though it appears to only be one. There is an element of zero-sumness that is introduced since you’re splitting the total rent.

Both seem reasonable assumptions. But this analysis is not full and complete, and it has raised many more questions and exploration paths. Perhaps I will revisit this in 2 years' time.